Klasyczne bramki logiczne - Algebra Boola

\[ \newcommand{\bra}[1]{\left \langle #1 \right \rvert} \newcommand{\ket}[1]{\left \rvert #1 \right \rangle} \newcommand{\braket}[2]{\left \langle #1 \middle \rvert #2 \right \rangle} \]

Obliczenia (przetwarzanie) wykonywane przez komputer możemy zdefiniować jako transformacje jednego stanu pamięci na inny. Z matematycznego punktu widzenia oznacza to, że obliczenia to funkcje, które przekształcają informacje.

W przypadku klasycznych komputerów podstawową jednostką pamięci jest bit (ang. binary digit). Funkcje, które operują na bitach nazywamy bramkami logicznymi (ang. logic gates).

Monety

Rozważmy monetę. Posiada ona dwie strony (odróżnialne od siebie). Kładąc monetę na podłożu możemy określić dostępne stany jako: \(\ket{O}\), \(\ket{R}\).

Posiadając dwie takie monety możemy określić cztery możliwe stany: \[\ket{OO}, \ket{OR}, \ket{RO}, \ket{RR}\]

Ponieważ pierwsza moneta ma dwa możliwe stany i druga moneta również ma dwie możliwości istnieją \(2\times 2= 2^{2} =4\) możliwe stany dla dwóch monet.

W przypadku trzech monet możemy określić osiem możliwych stanów: \[\ket{OOO}, \ket{OOR}, \ket{ORO}, \ket{ORR}, \ket{ROO}, \ket{ROR}, \ket{RRO}, \ket{RRR}\] Co daje nam \(2 \times 2 \times 2 = 2^{3}=8\) możliwych stanów.

dla \(n\) monet możemy określić \(2^{n}\) możliwych stanów.

Kości do gry

Kości do gry posiadają sześć stron. Każdej możemy przypisać liczbę od 1 do 6. Dwie kości do gry posiadają \(6 \times 6 = 36\) możliwych stanów. Idąc dalej, dla trzech kości do gry mamy \(6 \times 6 \times 6 = 6^{3} = 216\) możliwych stanów. Dla n kości do gry mamy \(6^{n}\) możliwych stanów.

Kodowanie informacji

Ile informacji możemy zakodować za pomocą monet i kości do gry?

Załóżmy, że chcemy przekazać informacje o jednym kolorze tęczy. Dla przypomnienia mamy 7 kolorów (czerwony, pomarańczowy, żółty, zielony, niebieski, indygo, fioletowy). Te 7 kolorów można zakodować (albo zareprezetować) poprzez różne konfiguracje monet i kości.

kolor	monety	kości
czerwony	OOO	11
pomarańczowy	OOR	12
żółty	ORO	13
zielony	ORR	14
niebieski	ROO	15
indygo	ROR	16
fioletowy	RRO	21

Pozostałe konfiguracje nie są używane (albo można w nich powtórzyć elementy do zakodowania).

Monety niosą mniej informacji niż kości do gry. Co prowadzi do ważnego wniosku: obiekt o dwóch stanach niesie najmniejszą (możliwą) ilość informacji. A co za tym idzie bit jest najmniejszą jednostką klasycznej informacji.

Zadanie: Angielski alfabet posiada 26 liter. Ile monet i kości potrzeba aby zakodować informacje o jednej literze?

Fizyczna realizacja klasycznych bitów

Obiekty fizyczne, które mogą przyjmować dwa stany:

przełącznik włączony/wyłączony
moneta
Płyty CD, DVD (ang. pits - wypalone laserem dziury, lands - nie wypalone dziury)
obwód elektryczny - może mieć dowolny prąd - ale wybieramy np. 0 lub 5V.

jak sprowadzić klasyfikację dla wielu klas do 2 klasowej?

Zazwyczaj oznaczamy te stany jako \(0\) i \(1\).

Zastosujmy nowe oznaczenia dla tych stanów: \[0 = \ket{0} \] oraz \[1 = \ket{1}\]

Reprezentacja binarna

W przypadku trzech monet mieliśmy następujące stany: \[OOO, OOR, ORO, ORR, ROO, ROR, RRO, RRR.\]

Możemy je zapisać w postaci binarnej jako: \[000, 001, 010, 011, 100, 101, 110, 111\] Dla przyzwyczajenia z zapisem możemy napisać również: \[\ket{000}, \ket{001}, \ket{010}, \ket{011}, \ket{100}, \ket{101}, \ket{110}, \ket{111}\]

Co oznacza, że możemy te stany zapisać matematycznie - łatwo nam nimi operować.

liczby tego typu nazywamy liczbami binarnymi, albo liczbami o podstawie 2.

Jak zapisujemy liczby w systemie dziesiętnym? i dlaczego nazywa się on dziesiętnym?

\[6174 = 6*1000 + 1*100 + 7*10 + 4*1 = 6*10^{3} + 1*10^{2} + 7*10^{1} +4*10^{0}\]

Natomiast: \[11010_{2} = 1*2^{4} + 1*2^{3} + 0*2^{2} + 1*2^{1} + 0*2^{0} \] co w systemie dziesiętnym daje nam: \(26\).

Zadanie: \(10111_{2}= ?_{10}\)

Zadanie: \(42= ?_{2}\)

Istnieje jeszcze wygodny system 16-tkowy (szesnastkowy) - gdzie współczynniki zapisujemy jako \(0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\).

Zadanie: \(F2A_{16}= ?_{10}\)

Jak zliczamy liczby w systemie dziesiętnym? a jak w dwójkowym?

Jak zapisać liczby ujemne i zmiennoprzecinkowe binarnie?

ASCII American Standard Code for Information Interchange

Komputer przechowuje informacje jako bity, jednak w naszym świecie używamy tekstu złożonego z liter. System ASCII przechowuje informacje o literach w postaci 7 bitowych liczb binarnych. W ten sposób możemy zapisać 128 znaków (liter, cyfr, znaków specjalnych) \(0000000\) do \(1111111\).

Znajdź w internecie tablicę ASCII i zapisz w kodzie ASCII swoje imię.

Standard UTF-8 (Unicode Transformation Format) przechowuje informacje o literach w postaci liczb binarnych do 32 bitów. co daje nam możliwość zapisania \(2^{32}=4294967296\) stanów. 128 pierwszych bitowych napisów w UTF-8 to kod ASCII.

Bramki logiczne

Bramki logiczne to funkcje Boolowskie, które możemy składać w bardziej złożone układy (ang. circuits). Stworzone przez George’a Boole’a w 1854 roku, algebra boola jest matematyczną strukturą, która opisuje zachowanie się obiektów, które mogą przyjmować tylko jedną z dwóch wartości: prawda lub fałsz. Zdolne są one do wykonywania np. dodawania, mnożenia czy też innych bardziej skomplikowanych operacji.

W latach trzydziestych XX wieku Claude Shannon zastosował algebrę boola do analizy i projektowania układów elektrycznych. Co oznacza, że zareprezentował on funkcje boolowskie za pomocą przełączników elektrycznych. Dlatego też komponenty elektroniczne odpowiadające funkcjom boolowskim nazywamy bramkami logicznymi.

Ciekawostka. Richard Feynman wykładał teorię obliczeń na Kalifornijskim Instytucie Technologii. Wykład ten prezentowany jest obecnie jako Feynmana wykłady o obliczeniach (ang. Feynman Lectures on Computation).

Z pozoru obliczenia przedstawione w ten sposób wyglądają jako abstrakcjny matematyczny koncept. Jednak jego realizacja zawsze wymaga jakiegoś układu fizycznego realizującego wykonywanie funkcji. Nie ma znaczenia jak ten układ zostanie zrealizowany: kule bilardowe, przełączniki elektroniczne, tranzystory, czy cokolwiek innego.

Logika obliczeń jest niezależna od realizacji bramek logicznych.

Z punktu widzenia realizacji zawsze chodzi nam o kontrolowany sposób zmiany stanu układu.

Na wykładzie postaramy się wskazać jak i kiedy logika klasycznych obliczeń może być uogólniona przez logikę obliczeń kwantowych. Jasne jest, że przypadek klasyczny powinien być szczególnym przypadkiem kwantowego.

obwody klasyczne

Zobaczmy jakie bramki możemy określić dla jednego bitu.

Bramki logiczne dla jednego bitu

Ile bramek mamy gdy input = 1 bit, output = 1 bit? Ile funkcji możemy zdefiniować dla odwzorowania jednego bitu w jeden bit?

Wszystkie cztery operatory działające na jednym bicie możemy określić jako:

Identyczność (ang. identity) - \(I(0)=0\), \(I(1)=1\)
Negacja (ang. negation, NOT, filps) - \(NOT(0)=1\), \(NOT(1)=0\)
Stałe zero \(ZERO(0)=0\), \(ZERO(1)=0\)
Stałe jeden \(ONE(0)=1\), \(ONE(1)=1\)

Po zastosowaniu operatora \(I\) oraz \(NOT\), z otrzymanego wyniku możemy wyznaczyc wartości początkowe. Jednak po zastosowaniu dwóch pozostałych operacji \(ZERO\) i \(ONE\) nie jesteśmy w stanie określic jaki był stan początkowy, który wygenerował określony wynik.

Te dwie własności pozwalają nam sklasyfikowac operatory jako:

Odwracalne - możemy odtworzyc wartośc początkową z wartości końcowej
Nieodwracalne - NIE możemy odtworzyc wartości początkowej z wartości końcowej.

Jak pokażemy później, wszystkie operatory reprezentujące kwantowe bramki będą odwracalne.

Inne bramki i operacje logiczne

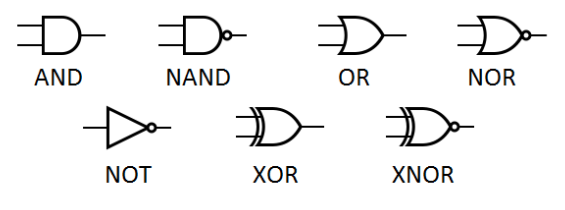
Zróbmy krótkie przedstawienie niektórych, klasycznych bramek logicznych.

Bramka logiczna jest implementacją funkcji boolowskiej. Operacją logiczną przeprowadzaną na jednym lub kilku binarnych wejściach produkującą jedną binarną wartość wyjściową. \[f: \{0,1\}^{n} \to \{0,1\} \]

Każdy element algebry boola (Boolean Statements) musi być określony jako prawda albo fałsz.

Bramki logiczne możemy wyrazić za pomocą tablicy prawdy (ang. truth table). Tablica ta posiada jedną kolumnę dla każdej zmiennej wejściowej oraz jedną kolumnę dla zmiennej wyjściowej. Kolumna wyjściowa przedstawia wszystkie możliwe wyniki przedstawianej logicznej operacji reprezentowanej przez tablicę. Każdy wiersz tablicy prawdy reprezentuje jedną możliwą kombinację (konfiguracje) danych wejściowych oraz wyniku.

Podstawowe bramki, które znasz to:

AND - koniunkcja
OR - alternatywa
NOT - negacja
NAND - not and
XOR - alternatywa wykluczająca (Exclusive OR) - dodawanie modulo 2

Zadanie: zapisz tablicę prawdy dla każdej bramki.

NOT gate

A	not A
0
1

AND gate

A	B	C
0	0
1	0
0	1
1	1

OR gate

A	B	C
0	0
1	0
0	1
1	1

NAND

A	B	C
0	0
1	0
0	1
1	1

XOR

A	B	C
0	0
1	0
0	1
1	1

Powyższe bramki pozwalają łączyć poszczególne elementy algebry boola ze sobą.

Zadanie: Porównaj AND oraz OR z potocznym znaczeniem tych słów.

Zadanie: Dlaczego Algebra boola nazywana jest algebrą zbiorów?

Zadanie: Czy składanie podzbiorów zbioru również generuje algebrę boola ?

Zadanie: ile bramek logicznych możemy stworzyć dla jednego bitu, dwóch bitów, trzech bitów?

Uniweralne bramki logiczne - NAND

Tak jak widzieliśmy dla 1-bitu informacji mieliśmy 4 bramki logiczne. Dla 2-bitów mieliśmy 16 bramek logicznych. Dla 3-bitów mamy już 256 możliwości.

W przypadku 2-bitów nie wypisaliśmy wszystkich bramek, dlaczego?

Czy musimy realizować wszystkie?

Na szczęście odpowiedź jest negatywna.

Istnieją tzw. zbiory bramek uniwersalnych dzięki którym możemy zrealizować dowolną funkcję boolowską.

NOT, AND, OR
NAND, AND
NAND
NOT, OR
NOR

Kody python

Zadanie 1: Napisz kod symuljący wyrzucenie symetrycznej monety \(100\), \(1000\), \(10000\) i \(100000\) razy

from random import randrange
# randrange(n) zwraca losową wartośc z przedziału (0,...,n-1)
# Twoje rozwiązanie

Zadanie 2: Napisz kod symulujący wyrzucenie niesymetrycznej monety gdzie prawdopodobieństwo wyrzucenia orła będzie wynosiło \(60\%\).

from random import randrange
# randrange(n) zwraca losową wartośc z przedziału (0,...,n-1)
# Twoje rozwiązanie

Szyfrowanie z wykorzystaniem bramki XOR

Weźmy dwie sekwencje bitów:

sekwencja A - przedstawiająca naszą zakodowaną wiadomośc: \[1 0 1 1 0 1 1 1 0 0 0\]

losowa sekwencja B: \[0 1 1 0 1 1 0 1 1 0 1\]

i obliczmy XOR między dwoma sekwencjami (dla poszczególnych kolumn) \(A\) XOR \(B\).

Zgodnie z tablicą prawdy dla XOR otrzymujemy: \[1 1 0 1 1 0 1 0 1 0 1\]

Na otrzymanym wyniku jeszcze raz zastosuj bramkę XOR.

Co możesz zauważyć?

Oblicz A XOR B XOR B.

Zamień wiadomość, którą chcesz zaszyfrować na binarną postać (czyli jako sekwencję zer i jedynek).

Weź losową sekwencję bitów (klucz szyfrujący), którą zna tylko nadawca i odbiorca.

\(1001011010...\) - wiadomość

\(0110101010...\) - klucz szyfrujący, czyli losowa sekwencja bitów

Zaszyfruj wiadomość wykonując operację XOR na każdym bicie wiadomości i klucza szyfrującego. Tak otrzymaną wiadomość (zaszyfrowaną) wyślij do odbiorcy.

decyrpting message

Odbiorca otrzymuje zaszyfrowaną wiadomość (posiada klucz szyfrujący).

Message XOR SecretSequence = EncryptedMessage

Message XOR SecretSequence XOR SecretSequence = Message

Nie powinniśmy używać SecretSequence więcej niż raz. Jeśli użyjemy jej więcej niż raz, to łatwo jest złamać szyfrowanie.

Dlaczego nie powinno się używać szyfru więcej niż jeden raz? Podpowiedź: Zakodowana wiadomość przestaje być losowa.

kody - rozwiązania zadań

from random import randrange
# randrange(n) zwraca losową wartośc z przedziału (0,...,n-1)
for experiment in [100,1000,10000,100000]:
    heads = tails = 0
    for i in range(experiment):
        if randrange(2) == 0: heads = heads + 1
        else: tails = tails + 1
    print("experiment:",experiment)
    print("heads =",heads,"  tails = ",tails)
    print("the ratio of #heads/#tails is",(round(heads/tails,4)))
    print() # empty line

from random import randrange

# let's pick a random number between {0,1,...,99}
# it is expected to be less than 60 with probability 0.6
#     and greater than or equal to 60 with probability 0.4
# ten sam przypadek możesz zrealizować dla losowania wartosci rzeczywistej
# pomiędzy 0 i 1.

for experiment in [100,1000,10000,100000]:
    heads = tails = 0
    for i in range(experiment):
        if randrange(100) <60: heads = heads + 1 # with probability 0.6
        else: tails = tails + 1 # with probability 0.4
    print("experiment:",experiment)
    print("heads =",heads,"  tails = ",tails)
    print("the ratio of #heads/#tails is",(round(heads/tails,4)))
    print() # empty line