Pennylane wprowadzenie

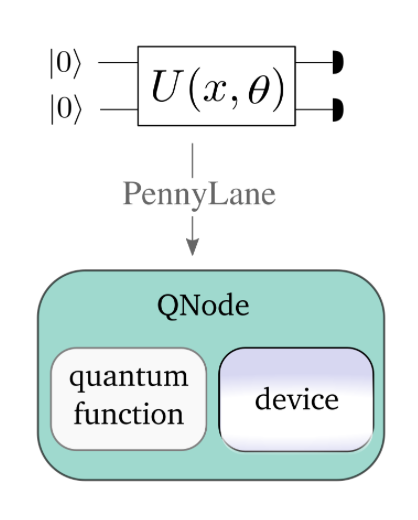
Obiekt Qnode będziemy używać do definicji obwodów kwantowych. Obiekt ten wspiera wiele bibliotek do obliczeń numerycznych, tzw. interfejsów: - NumPy, - PyTorch, - TensorFlow, - JAX

Domyślnie QNodes używa interfejs NumPy. Dzięki niemu mamy dostęp do optymalizatorów domyślnych z biblioteki Pennylane. Pozostałe interferjsy wymagają użycia optymalizatorów z innych pakietów.

PennyLane oferuje kilka symulatorów: - ‘default.qubit’, - ‘default.mixed’, - ‘lightning.qubit’, - ‘default.gaussian’, - ‘default.clifford’, - ‘default.tensor’

Kod Pennylane

Pennylane pozwala zrealizować obwód kwantowy (ang. quantum circuit) jako funkcję w Pythonie.

import pennylane as qml

def qc(): # from quantum circuit
    qml.Hadamard(wires=0)
    return qml.counts()

wires oznacza kwantowy podsystem - czyli nasz pojedynczy kubit. Liczymy od 0 nie od 1.

Funkcja kwantowa może pobierać klasyczne pamaretry
Funkcja kwantowa może zawierać klasyczny flow (przepływ) twojego programu for czy if else.

Zbiór kwantowych operatorów

Uruchomienie obwodu kwantowego

Uruchomienie odbywa się po wyborze device z określeniem ilości kubitów (wires)

# domyślnie
dev = qml.device("default.qubit", wires=1)

# można nadać własne nazwy kubitów
dev_unique_wires =  qml.device("default.qubit", wires=['q1','aux'])

W przypadku gdy będziemy chcieli powtórzyć wielokrotnie wykonanie obwodu w celu zebrania statystyki wyników mozemy zdefiniować parametr shots

# shots 
shots_list = [5,10,1000]
dev = qml.device("default.qubit", wires=1, shots=shots_list)

qml.QNode - łączy naszą kwantową funkcję ze środowiskiem na którym chcemy ją wykonać

circ = qml.QNode(qc, dev)

circ()

({'0': tensor(2, requires_grad=True), '1': tensor(3, requires_grad=True)},
 {'0': tensor(6, requires_grad=True), '1': tensor(4, requires_grad=True)},
 {'0': tensor(486, requires_grad=True), '1': tensor(514, requires_grad=True)})

Łatwiej skorzystać z dekoratora @qml.qnode bezpośrednio przy definicji funkcji kwantowej

dev = qml.device("default.qubit", wires=1, shots=1000)
@qml.qnode(dev)
def circuit():
    qml.Hadamard(wires=0)
    return qml.counts()

circuit()

{'0': tensor(505, requires_grad=True), '1': tensor(495, requires_grad=True)}

Konstrukcja obwodów kwantowych w Pennylane

Na ostatnich zajęciach wyprodukowaliśmy klasyczną i kwantową sieć neuronową realizowaną w bibliotece PyTorch i Pennylane.

Kod naszej wartwy ukrytej w której użyliśmy obwodu kwantowego realizował następujące obiekty i funkcje:


import pennylane as qml

n_qubits = 2
dev = qml.device("default.qubit", wires=n_qubits)

@qml.qnode(dev)
def qnode(inputs, weights):
    qml.AngleEmbedding(inputs, wires=range(n_qubits))
    qml.BasicEntanglerLayers(weights, wires=range(n_qubits))
    return [qml.expval(qml.PauliZ(wires=i)) for i in range(n_qubits)]

Obwody kwantowe składają się z rejestrów, które reprezentują poszczególne kubity.

Domyślnie kubity inicjalizujemy w stanie 0.

Liczbę rejestrów możesz ustalić parametrem wires przy definicji środowiska wykonawczego device.

dev = qml.device("default.qubit", wires=1)

Operacje wykonywane na kubitach nazywamy bramkami.

Operacje te można wykonywać na jednym albo i wielu kubitach na raz.

Domyślnie będziemy optymalizować algortymy aby składały się z jak najmniejszej ilości bramek działających na dużą liczbę kubitów.

Graficznie można rozumieć realizację algorytmu jako stosowanie bramek na poszczególnych kubitach.

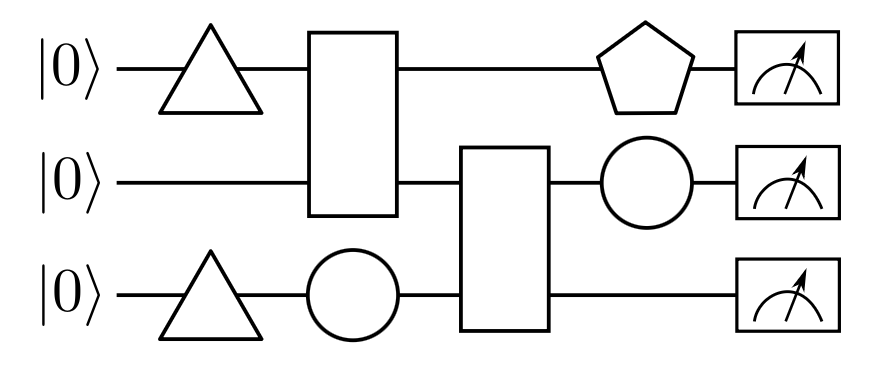
W bibliotece PennyLane, obwody kwantowe reprezentowane są przez kwantowe funkcje, realizowane przez klasyczne funkcje w pythonie.

Schemat kodu penny lane możemy zapisać jako:

import pennylane as qml

def my_quantum_function(params):

    # Single-qubit operations with no input parameters
    qml.Gate1(wires=0)
    qml.Gate2(wires=1)

    # A single-qubit operation with an input parameter
    qml.Gate3(params[0], wires=0)

    # Two-qubit operation with no input parameter on wires 0 and 1
    qml.TwoQubitGate1(wires=[0, 1])

    # Two-qubit operation with an input parameter on wires 0 and 1
    qml.TwoQubitGate2(params[1], wires=[0, 1])

    # Return the result of a measurement
    return qml.Measurement(wires=[0, 1])

Przykładowo


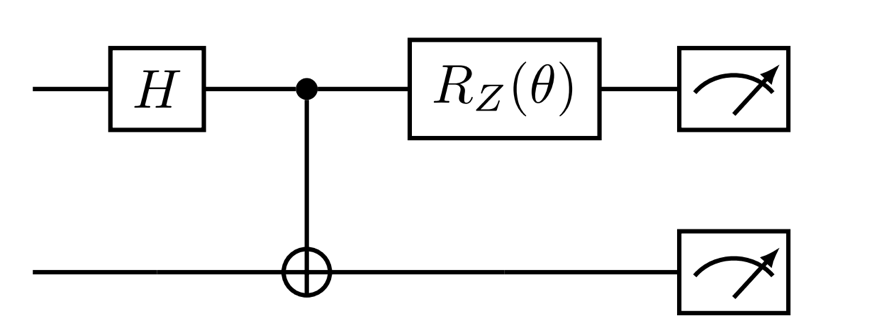
def my_first_circuit(theta):

    qml.Hadamard(wires = 0)
    qml.CNOT(wires = [0,1])
    qml.RZ(theta, wires = 0)

    return qml.probs(wires = [0,1])

Matematycznie całość możemy zapisać jako:

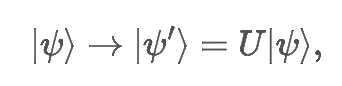
import pennylane as qml
from pennylane import numpy as np

dev = qml.device("default.qubit", wires=2)
#dev = qml.device("default.qubit", wires=2, shots=1000)

@qml.qnode(dev)
def circ(theta):
    qml.Hadamard(wires = 0)
    qml.CNOT(wires = [0,1])
    qml.RZ(theta, wires = 0)
    return qml.state()
#    return qml.probs(wires = [0,1])

circ(np.pi)

tensor([4.32978028e-17-0.70710678j, 0.00000000e+00+0.j        ,
        0.00000000e+00+0.j        , 4.32978028e-17+0.70710678j], requires_grad=True)

print(qml.draw(circ)(np.pi))

0: ──H─╭●──RZ(3.14)─┤  State
1: ────╰X───────────┤  State

qml.draw_mpl(circ)(np.pi)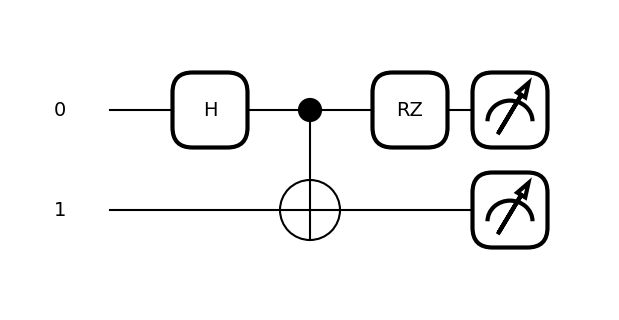

import matplotlib.pyplot as plt
qml.drawer.use_style("sketch")
fig, ax = qml.draw_mpl(circ)(np.pi)
plt.show()

qml.drawer.use_style("pennylane_sketch")
fig, ax = qml.draw_mpl(circ)(np.pi)
plt.show()

Matplotlib is building the font cache; this may take a moment.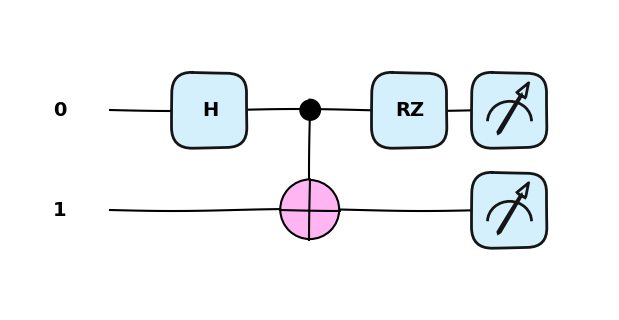

Obwody z jednym kubitem

\[ \ket{\psi}=\ket{0} \] Przedstawmy obwód kwantowy z jednym kubitem. Funkcja kwantowa zwraca nam stan kubitu po realizacji obwodu.

Obwód z jednym kubitem bez bramek.

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)
def qc():
    return qml.state()

qc()

tensor([1.+0.j, 0.+0.j], requires_grad=True)

wektor \([1,0]\) można interpretować jako stan \(\ket{0}\) czyli jako wartość bitu \(0\).

Natomiast wykorzystując metodę qml.probs() możesz zwrócić kwadraty amplitud czyli prawdopodobieństow otrzymania 0 i 1.

import pennylane as qml

dev = qml.device("default.qubit", wires=1)

@qml.qnode(dev)
def qc2():
    return qml.probs(wires=0)

qc2()

tensor([1., 0.], requires_grad=True)

Zobaczmy jak zainicjalozować stan \(\ket{1}= [0,1]^T\) \[ \ket{\psi}=\ket{1} \]

from pennylane import numpy as np
from pennylane.ops import StatePrep

stan = np.array([0,1]) # stan do inicjalizacji

@qml.qnode(dev)
def qc():
    StatePrep(stan, wires=0)
    return qml.state()

qc()

tensor([0.+0.j, 1.+0.j], requires_grad=True)

@qml.qnode(dev)
def qc():
    StatePrep(stan, wires=0)
    return qml.probs()

qc()

tensor([0., 1.], requires_grad=True)

utwórzmy pełną superpozycję stanu 0 i 1. \[ \ket{\psi}=\frac{1}{\sqrt{2}} (\ket{0} + \ket{1} ) \]

stan = np.array([1/np.sqrt(2), 1/np.sqrt(2)])

@qml.qnode(dev)
def qc_s():
    qml.StatePrep(stan,wires=0)
    return qml.state()

print(f"amplitudy: {qc_s()}")


@qml.qnode(dev)
def qc_p():
    qml.StatePrep(stan,wires=0)
    return qml.probs()

print(f"prwadopodobieństwa: {qc_p()}")

print(f"test czy amp^2 = prawdopodobienstwo: {qc_s()**2 == qc_p()}")

amplitudy: [0.70710678+0.j 0.70710678+0.j]
prwadopodobieństwa: [0.5 0.5]
test czy amp^2 = prawdopodobienstwo: [ True  True]

Stany dwukubitowe

\[ \ket{\psi}=\ket{00} \] \[ \ket{\psi}=\ket{01} \] \[ \ket{\psi}=\ket{10} \] \[ \ket{\psi}=\ket{11} \]

dev = qml.device("default.qubit", wires=2)
@qml.qnode(dev)
def qc():
    return qml.state()

qc()

tensor([1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j], requires_grad=True)

\[ \ket{\psi}=\frac{1}{2}\left( \ket{00} + \ket{01} + \ket{10} + \ket{11} \right) \]

dev = qml.device("default.qubit", wires=2)

stan = np.array([1/2, 1/2, 1/2, 1/2])

prawd = [i**2 for i in stan]
print(f"test: suma prawdopodobienst {np.sum(prawd)}")

@qml.qnode(dev)
def qc():
    StatePrep(stan, wires=[0,1])
    return qml.state()

qc()

test: suma prawdopodobienst 1.0

tensor([0.5+0.j, 0.5+0.j, 0.5+0.j, 0.5+0.j], requires_grad=True)

ZADANIE Napisz funkcję generującą stan jednego kubitu jako funkcję kąta \(\theta\)

def stan_kubitu(theta):
    pass # Twoj kod

\(\ket{\psi}= [\cos(\frac{\theta}{2}), \sin(\frac{\theta}{2})]\)

Wygeneruj obwód z pojedynczym kubitem inicjalizujący stan \(\ket{0}\) , \(\ket{1}\) oraz \(\frac{1}{\sqrt{2}} (\ket{0} + \ket{1} )\)

Bramki jako operacje na kubitach

Bramka X

Bramka X-gate reprezentowana jest przez macierz Pauli-X :

\[ X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix} \]

Bramka X obraca kubit w kierunku osi na sferze Bloch’a o \(\pi\) radianów. Zmienia \(|0\rangle\) na \(|1\rangle\) oraz \(|1\rangle\) na \(|0\rangle\). Jest często nazywana kwantowym odpowiednikiem bramki NOT lub określana jako bit-flip.

\[ \sigma_x \ket{0} = \ket{1} \,\,\, \sigma_x\ket{1} = \ket{0} \]

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)
def qc():
    qml.X(wires=0)
    return qml.state()

qc()

tensor([0.+0.j, 1.+0.j], requires_grad=True)

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)
def qc():
    qml.PauliX(wires=0)
    return qml.state()

qc()

tensor([0.+0.j, 1.+0.j], requires_grad=True)

qml.draw_mpl(qc)()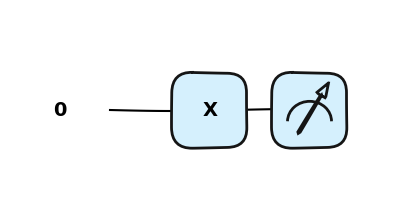

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)
def qc():
    qml.PauliX(wires=0)
    qml.X(wires=0)
    return qml.state()

qml.draw_mpl(qc)()
qc()

tensor([1.+0.j, 0.+0.j], requires_grad=True)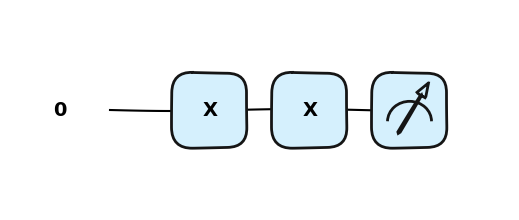

Jak bramka X działa na stan \(\ket{+}\), \(\ket{-}\) \(\ket{i}\) i \(\ket{-i}\)

Dowolna bramka unitarna

from pennylane import numpy as np

U = np.array([[1, 1], [1, -1]]) / np.sqrt(2)

dev = qml.device("default.qubit", wires=1)

@qml.qnode(dev)
def qc():
    qml.QubitUnitary(U, wires=0)
    return qml.state()

qml.draw_mpl(qc)()
qc()

Bramka Hadamarda

Bramka Hadamarda przetwarza stan \(|0\rangle\) na kombinacje liniowa (superpozycje) \(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\), co oznacza, że pomiar zwróci z takim samym prawdopodobieństwem stanu 1 lub 0. Stan ten często oznaczany jest jako: \(|+\rangle\).

\[ H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \\ \end{pmatrix} \]

\[ H\ket{0} = \frac{\sqrt{2}}{2} (\ket{0}+ \ket{1})\] \[ H\ket{1} = \frac{\sqrt{2}}{2}(\ket{0}- \ket{1})\]

dev = qml.device("default.qubit", wires=1)

@qml.qnode(dev)
def qc():
    qml.Hadamard(wires=0)
    return qml.state()

qc()

dev = qml.device("default.qubit", wires=1)

@qml.qnode(dev)
def qc():
    qml.Hadamard(wires=0)
    qml.Hadamard(wires=0)
    return qml.state()

qc()

dev = qml.device("default.qubit", wires=1)

@qml.qnode(dev)
def qc(state):
    if state==1:
        qml.X(wires=0)
    qml.Hadamard(wires=0)
    qml.PauliX(wires=0)
    qml.Hadamard(wires=0)
    return qml.state()

qc(0)

qc(1)

bramka SX

Bramka SX jest pierwiastkiem kwadratowym bramki X. Dwukrotne zastosowanie powinno reazlizowac bramkę X.

\[ SX = \frac{1}{2}\begin{pmatrix} 1+i & 1-i \\ 1-i & 1+i \\ \end{pmatrix} \]

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)
def qc():
    qml.SX(wires=0)
    return qml.state()

qml.draw_mpl(qc)()
qc()

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)
def qc():
    qml.SX(wires=0)
    qml.SX(wires=0)
    return qml.state()

qml.draw_mpl(qc)()
qc()

Z gate

\[ Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & e^{i \pi} \\ \end{pmatrix} \]

Inne nazwy bramki: phase flip lub sign flip

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)
def qc():
    qml.Z(wires=0)
    return qml.state()

qml.draw_mpl(qc)()
qc()

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)
def qc():
    qml.PauliZ(wires=0)
    return qml.state()

qml.draw_mpl(qc)()
qc()

Jak bramka Z działa na stan \(\ket{+}\), \(\ket{-}\) \(\ket{i}\) i \(\ket{-i}\) ?

Jak zmieniają się prawdopodobieństwa wyników w bazie obliczeniowej?

RZ gate

Bramkę PauliZ można uogólnić i sparametryzować kątem. Dla \(\phi=\pi\) otrzymujemy bramkę \(\sigma_z\).

\[ \begin{pmatrix} 1 & 0 \\ 0 & -1 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & e^{i \pi} \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & e^{i \phi} \\ \end{pmatrix} \]

\[ R_Z(\phi) = e^{-i \phi \frac{\sigma_z}{2} } \]

\[ RZ = \begin{pmatrix} e ^{-i \frac{\phi}{2} } & 0 \\ 0 & e ^{i \frac{\phi}{2} } \\ \end{pmatrix} = \cos(\frac{\phi}{2})I_2 - \sin(\frac{\phi}{2}) i\sigma_z \]

from pennylane import numpy as np

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)


def qc(phi):
    qml.RZ(phi=phi, wires=0)
    return qml.state()

qc(np.pi/2)

qml.draw_mpl(qc)(np.pi/2)

from pennylane import numpy as np

dev = qml.device("default.qubit", wires=1)
@qml.qnode(dev)


def qc(phi):
    qml.SX(wires=0)
    qml.RZ(phi=phi, wires=0)
    return qml.state()

qc(np.pi)

Znajdz informacje o bramce \(S\), \(S^{\dag}\), \(T\), \(T^{\dag}\).