Modele uczenia maszynowego

Rozwój technologii i powszechna cyfryzacja przyczyniły się do powstania nowego zasobu, jakim są dane. Dane te są generowane i przetwarzane zarówno w sposób ustrukturyzowany, jak i nieustrukturyzowany. Strukturyzacja danych doprowadziła do rozwoju wielu modeli, które dziś ogólnie określamy jako modele uczenia maszynowego (ang. machine learning, ML). Natomiast przetwarzanie danych nieustrukturyzowanych takich jak tekst, obrazy czy wideo, przyczyniło się do rozwoju uczenia głębokiego (ang. deep learning, DL). Oba te podejścia często określane zbiorczo jako sztuczna inteligencja (ang. artificial inteligence, AI), zostały stworzone głównie do rozpoznawania wzorców. Jednak coraz częściej wykorzystywane są również do modelowania i generowania nowych danych. Klasyczny model sztucznej inteligencji możemy wyrazić jako funkcję \(f(X,\theta)\), która zależy zarówno od danych reprezentowanych przez ustrukturyzowaną macierz \(X\), jak i od parametrów \(\theta\), których wartości zostają ustalone w procesie uczenia.

W uczeniu nadzorowanym posiadamy wartości zmiennej celu dla wygenerowanych danych treningowych. Dwa podstawowe modele nadzorowanego uczenia maszynowego możemy zrealizować jako proste sieci neuronowe.

Do wygenerowania kodów użyjemy biblioteki PyTorch

Regresja liniowa

Wygenerujemy niezaszumione dane na podstawie wzoru \(y = 2 x - 1\). Na podstawie zbioru danych postaramy się oszacować nieznane parametry czyli wyraz przy \(x\) (\(\alpha_1 = 2\)) i wyraz wolny (\(\alpha_0 = -1\)).

import numpy as np
import matplotlib.pyplot as plt

# zbior danych
x = range(11)
y = [2*xi - 1 for xi in x]
plt.plot(x, y, 'go', label='True data', alpha=0.5)

Model regresji liniowej dla jednej zmiennej można zrealizować jako prostą jednowarstwową sieć neuronową. Cały proces można zrealizować za pomocą obiektu torch.nn.Linear

import torch

class LinearRegression(torch.nn.Module):

    def __init__(self, inputSize, outputSize):
        super(LinearRegression, self).__init__()
        self.layers = torch.nn.Sequential(
            torch.nn.Linear(inputSize, outputSize)
        ) 
        
    def forward(self, x):
        return self.layers(x)

m = torch.nn.Linear(1,1)

m

Linear(in_features=1, out_features=1, bias=True)

m.weight, m.bias

(Parameter containing:
 tensor([[-0.3386]], requires_grad=True),
 Parameter containing:
 tensor([-0.7039], requires_grad=True))

Aby nasze dane mogłybyć przeliczane przez bibliotekę PyTorch musimy je przetworzyć na tensory - czyli obiekty z biblioteki PyTorch.

# dostosowanie do pytorch
x = np.array(x, dtype=np.float32)
y = np.array(y, dtype=np.float32)

X_train = torch.from_numpy(x).view(-1,1)
y_train = torch.from_numpy(y).view(-1,1)

Uwaga - ponieważ mamy jedną zmienną zawierającą 10 przypadków - potrzebujemy listy składającej się z 10 list jednoelementowych.

Mozna tez wykorzystac obiektowe programowanie.

from torch.utils.data import Dataset, DataLoader

class LinearDataset(Dataset):
    def __init__(self, X_train, y_train):
        self.X_train = X_train # tensor typu torch
        self.y_train = y_train

    def __len__(self):
        return len(self.y_train)

    def __getitem__(self, idx):
        return self.X_train[idx], self.y_train[idx]

dataset = LinearDataset(X_train=X_train, y_train=y_train)

dataloader = DataLoader(dataset, shuffle=True, batch_size=2)

Możemy utworzyć model i wybrać optymalizator z funkcją kosztu.

# obiekt liniowej regresji w wersji sieci nn
lr_model = LinearRegression(1,1)

criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(lr_model.parameters(), lr=0.01)

Możemy sprawdzić, że nasz model będzie dostrajał 2 parametry.

num_params = sum(p.numel() for p in lr_model.parameters() if p.requires_grad)
print(f"liczba trenowalnych parametrów: {num_params}")

liczba trenowalnych parametrów: 2

Parametry te w początkowej inicjalizacji mają następujące wartości:

for layer in lr_model.layers:
    if isinstance(layer, torch.nn.Linear):
        print(f"weight: {layer.state_dict()['weight']}")
        print(f"bias: {layer.state_dict()['bias']}")

weight: tensor([[0.5697]])
bias: tensor([-0.6299])

epochs = 400
# petla uczaca 
for epoch in range(epochs):
    lr_model.train() # etap trenowania 

    y_pred = lr_model(X_train)
    loss = criterion(y_pred, y_train)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if (epoch+1) % 50 == 0:
        print(f'epoch: {epoch+1:03d}, loss = {loss.item():.4f}')
 
    lr_model.eval() # etap ewaluacji modelu

# po treningu jeszcze raz generujemy predykcje
lr_model.eval()
with torch.no_grad():
    predicted = lr_model(X_train)

epoch: 050, loss = 0.0525
epoch: 100, loss = 0.0299
epoch: 150, loss = 0.0171
epoch: 200, loss = 0.0097
epoch: 250, loss = 0.0056
epoch: 300, loss = 0.0032
epoch: 350, loss = 0.0018
epoch: 400, loss = 0.0010

Mozna tez wykorzystac obiekt dataloader

for epoch in range(50):
    for X_batch, y_batch in dataloader:
        preds = lr_model(X_batch)
        loss = criterion(preds, y_batch)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    if epoch % 10 == 0:
        print(f"Epoch {epoch}, loss = {loss.item():.4f}")

Epoch 0, loss = 0.0004
Epoch 10, loss = 0.0000
Epoch 20, loss = 0.0001
Epoch 30, loss = 0.0001
Epoch 40, loss = 0.0001

Otrzymane parametry po uczeniu

print(f"po procesie uczenia waga: {lr_model.layers[0].weight} oraz bias {lr_model.layers[0].bias}")

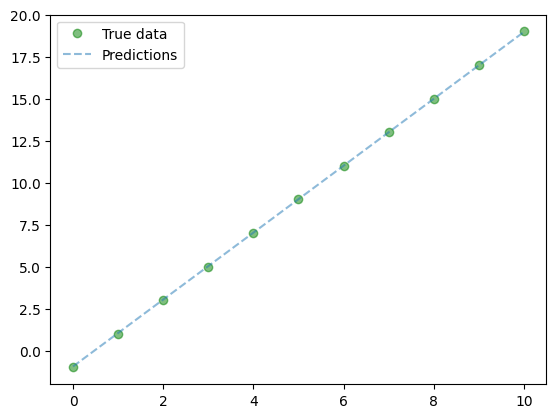
po procesie uczenia waga: Parameter containing:
tensor([[1.9981]], requires_grad=True) oraz bias Parameter containing:
tensor([-0.9894], requires_grad=True)

Dopasowanie modelu do danych można przedstawić na wykresie

plt.clf()
plt.plot(X_train, y_train, 'go', label='True data', alpha=0.5)
plt.plot(X_train, predicted, '--', label='Predictions', alpha=0.5)
plt.legend(loc='best')
plt.show()

import torch
import pandas as pd 
import matplotlib.pyplot as plt
from IPython.display import clear_output

torch.manual_seed(1234)

# DANE 
x = torch.linspace(0,10,500).view(-1,1)
y = torch.sin(x)
y = y + 0.1*(torch.rand(500).view(-1,1)-0.5)

plt.figure(figsize=(8,4))
plt.plot(x, torch.sin(x).view(-1,1), color="tab:grey", alpha=0.6, label="sin(x)")
plt.scatter(x,y, label="dane treningowe")
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()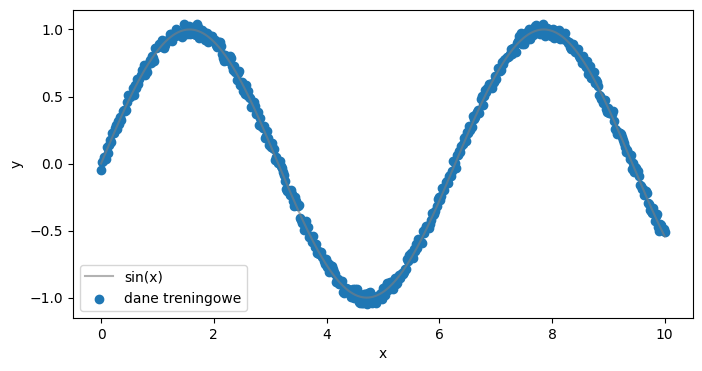

class SinusEstimator(torch.nn.Module):

    def __init__(self, N_INPUT: int, N_OUTPUT: int):
        super(SinusEstimator,self).__init__()
        self.layers = torch.nn.Sequential(
            torch.nn.Linear(N_INPUT, 64),
            torch.nn.ReLU(),
            torch.nn.Linear(64,32),
            torch.nn.ReLU(),
            torch.nn.Linear(32,16),
            torch.nn.Tanh(),
            torch.nn.Linear(16,N_OUTPUT)
        )


    def forward(self, x):
        x = self.layers(x)
        return x

model = SinusEstimator(1,1)

learning_rate=0.001
optimiser = torch.optim.Adam(model.parameters(), lr=learning_rate)
criterion = torch.nn.MSELoss()

losses = []

def callback(model, loss):
    losses.append(loss.item())

    clear_output(wait=True)
    prediction = model(x).detach()
    plt.figure(figsize=(6,2.5))
    plt.plot(x[:,0].detach(), torch.sin(x)[:,0].detach(), label="Exact solution", color="tab:grey", alpha=0.6)
    plt.plot(x[:,0].detach(), prediction[:,0], label="Classical solution", color="tab:green")
    plt.title(f"Training step {len(losses)}")
    plt.legend()
    plt.show()

    plt.figure(figsize=(6,2.5))
    plt.title('Lossfn Visualised')
    plt.plot(losses)
    plt.show()

def train(X,Y, model, optimiser, epochs, lossfn, callback = None):
    for epoch in range(epochs):
        model.train()
        prediction = model(X)
        loss = lossfn(prediction, Y)

        optimiser.zero_grad()
        loss.backward()
        optimiser.step()
        model.eval()
        if callback != None:
            callback(model, loss)

x_train = x.requires_grad_(False)

train(x_train, y, model, optimiser, 300, criterion, callback)

def mse(y, y_pred) -> torch.Tensor:
    return torch.mean((y-y_pred)**2)

def special_loss_fn(y, y_pred) -> torch.Tensor:
    return mse(y, y_pred) + torch.mean((y_pred - torch.sin(x))**2)

model2 = SinusEstimator(1,1)

learning_rate=0.001
optimiser = torch.optim.Adam(model2.parameters(), lr=learning_rate)
criterion = torch.nn.MSELoss()
losses = []

train(x_train, y, model2, optimiser, 200, special_loss_fn, callback)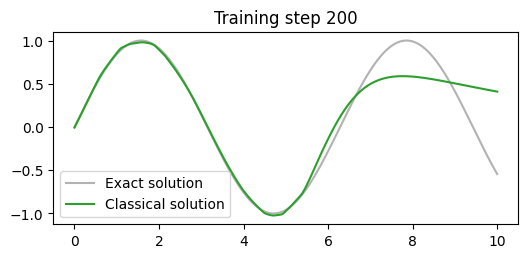

Regresja logistyczna

W przypadku procesu klasyfikacji danych do numerycznego wyniku musimy dodać funkcję aktywacji - sigmoid \(\sigma\), która pozwoli nam wygenerować prawdopodobieństwo otrzymania klasy 1.

Dane wygenerujemy na podstawie pakietu scikit-learn

from sklearn.datasets import make_classification
import numpy as np

# prepare dataset
X, y = make_classification(n_samples=10**4, n_features=10 ,random_state=42)

import torch

class LogisticRegression(torch.nn.Module):

    def __init__(self, inputSize, outputSize):
        super(LogisticRegression, self).__init__()
        self.layers = torch.nn.Sequential(
            torch.nn.Linear(inputSize, outputSize),
            torch.nn.Sigmoid()
        )

    def forward(self, x):
        logits = self.layers(x)
        return logits

Podobnie jak w przypadku regresji liniowej musimy przetworzyć nasze dane do obiektów torch.

X_train = torch.from_numpy(X.astype(np.float32))
y_train = torch.from_numpy(y.astype(np.float32))
y_train = y_train.view(y_train.shape[0], 1)

model = LogisticRegression(X_train.shape[1], y_train.shape[1])

learningRate = 0.01
criterion = torch.nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learningRate)

# petla uczaca 
num_epochs = 500

for epoch in range(num_epochs):
    # forward pass and loss
    model.train()
    y_predicted = model(X_train)
    loss = criterion(y_predicted, y_train)
    
    loss.backward()
    optimizer.step()
    optimizer.zero_grad()
    model.eval()

    if (epoch+1) % 50 == 0:
        print(f'epoch: {epoch+1}, loss = {loss.item():.4f}')



model.eval()
with torch.no_grad():
    y_predicted = model(X_train)  # no need to call model.forward()
    y_predicted_cls = y_predicted.round()   # round off to nearest class
    acc = y_predicted_cls.eq(y_train).sum() / float(y_train.shape[0])  # accuracy
    print(f'accuracy = {acc:.4f}')
    print(f"predykcja dla wiersza 0:{y_predicted[0]}, wartosc prawdziwa: {y_train[0]}")

epoch: 50, loss = 0.6307
epoch: 100, loss = 0.5104
epoch: 150, loss = 0.4487
epoch: 200, loss = 0.4120
epoch: 250, loss = 0.3878
epoch: 300, loss = 0.3708
epoch: 350, loss = 0.3581
epoch: 400, loss = 0.3484
epoch: 450, loss = 0.3406
epoch: 500, loss = 0.3343
accuracy = 0.8830
predykcja dla wiersza 0:tensor([0.8189]), wartosc prawdziwa: tensor([1.])